2.9 赋值
虽然大多数程序不需要用到赋值，但是有时候，对顶级变量或者由 let、lambda 绑定的变量进行赋值是很有用的。赋值并不像let或lambda一样创建新的绑定，而是修改已经存在的绑定。赋值通过set!来进行。
(define abcde '(a b c d e))
abcde => (a b c d e)
(set! abcde (cdr abcde))
abcde => (b c d e)
(let ([abcde '(a b c d e)])
(set! abcde (reverse abcde))
abcde) => (e d c b a)
很多语言需要使用赋值来初始化本地变量，声明变量与绑定变量是分开的。在 Scheme 里，所有的本地变量在绑定时立即被赋予一个值。Besides making the separate assignment to initialize local variables unnecessary, 它确保程序员不会忘记初始化它们，在大多数语言里，这是很常见的错误。
事实上，对于其它语言是必需的、方便的赋值，对 Scheme 而言却是不必要的，也是不方便的。因为，通常存在着更清晰的不使用赋值的方式来表达相同的算法。One common practice in some language is to sequence expression evaluation with a series of assignments, 比如，下面的函数计算一个二次方程的根
(define quadratic-formula
(lambda (a b c)
(let ([root1 0] [root2 0] [minusb 0] [radical 0] [divisor 0])
(set! minusb (- 0 b))
(set! radical (sqrt (- (* b b) (* 4 (* a c)))))
(set! divisor (* 2 a))
(set! root1 (/ (+ minusb radical) divisor))
(set! root2 (/ (- minusb radical) divisor))
(cons root1 root2))))
根的计算依据二次方程公式
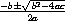
计算出 0 = ax2 + bx + c 的解。在这个函数里，let用于单独创建对其它语言而言所必需的变量。开头的三个赋值表达式分别计算公式中的 -b,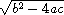 
, 以及 2a。最后两个赋值表达式分别计算两个根。由两个根构成的点对就是quadratic-formula的值。例如，2x2 - 4x - 6 的根分别是 x = 3 以及 x = -1.
(quadratic-formula 2 -4 -6) => (3 . -1)
上面的函数可以工作，但是可以用更清晰的方式来实现，不使用赋值
(define quadratic-formula
(lambda (a b c)
(let ([minusb (- 0 b)]
[radical (sqrt (- (* b b) (* 4 (* a c))))]
[divisor (* 2 a)])
(let ([root1 (/ (+ minusb radical) divisor)]
[root2 (/ (+ minusb radical) divisor)])
(cons root1 root2)))))
在这个版本里，赋值表达式不见了，然而本质上依然是相同的算法。通过使用两个let表达式，更为清晰地表现了root1及root2与 minusb, radical, divisor 的关系。同样重要的是，the let expressions make clear the lack of dependencies among minusb, radical, and divisor and between root1 and root2.
在 Scheme 里，赋值确实有某些用途，要不然，语言就不会支持它了。思考下面这个版本的cons，它对自己被调用的次数进行计数，用来计数的变量叫做 cons-count。它使用 set!来使计数递增。要实现相同的行为，不使用赋值是不行的。
(define kons-count 0)
(define kons
(lambda (x y)
(set! kons-count (+ kons-count 1))
(cons x y)))
(kons 'a '(b c)) => (a b c)
kons-count => 1
(kons 'a (kons 'b (kons 'c '()))) => (a b c)
kons-count => 4
赋值通常用来实现需要保持内部状态的函数。例如，假设我们需要定义一个函数，当它第一次调用的时候返回0,第二次调用的时候返回1, 第三次调用的时候返回2,依次递增。我们可以使用类似于上面的 kons 函数的写法，使用一个全局变量来保存状态：
(define next 0)
(define count
(lambda ()
(let ([v next])
(set! next (+ next 1))
v)))
(count) => 0
(count) => 1
这个解决方案不是很好，变量next是全局可见的，这是没必要的。因为它对所有函数都是可见的，系统里的任何代码都可以改变它的值，可能会在不经意间改变count函数的行为。我们可以使用let表达式将它绑定在lambda表达式的外面，来解决这个问题：
(define count
(let ([next 0])
(lambda ()
(let ([v next])
(set! next (+ next 1))
v))))
使用后一个解决方案可以很容易地同时使用多个计数器，互不干扰。因为每个函数的计数变量都是函数内部的本地变量(这就是所谓的闭包)。下面的函数 make-counter每次被调用的时候返回一个新的计数函数（注意，这就是所谓的高阶函数）
(define make-counter
(lambda ()
(let ([next 0])
(lambda ()
(let ([v next])
(set! next (+ next 1))
v)))))
next绑定在make-counter内部，但是却又处在被 return 的 lambda外部，由 make-counter “制造”出来的每一个函数都有自己的计数器，互不干扰。
(define count1 (make-counter))
(define count2 (make-counter))
(count1) => 0
(count2) => 0
(count1) => 1
(count1) => 2
(count2) => 1
如果一个状态变量需要在多个函数之间共享，但是我们又不希望它是全局可见的，我们可以使用let绑定变量，然后使用set!使得函数在顶级是可见的。
(define shhh #f)
(define tell #f)
(let ([secret 0])
(set! shhh
(lambda (message)
(set! secret message)))
(set! tell
(lambda ()
secret)))
(shhh "sally likes harry")
(tell) => "sally likes harry"
secret => exception: variable secret is not bound
「点评：这两个函数真令人惊叹，变魔术一般变出两个函数，而且它们还共享一个共同的变量」
在对变量赋值之前需要先定义，所以，我们先把 shhh及tell定义成 #f。 (Any initial value would do.) We'll see this structure again in Section 3.5 and a better way to structure code like this as a library in Section 3.6.
有时候，保存本地状态是有用的，可以缓存计算结果以及实现惰性求值。only once and only on demand. The procedure lazy below accepts a thunk, or zero-argument procedure, as an argument. Thunks are often used to "freeze" computations that must be delayed for some reason, which is exactly what we need to do in this situation. When passed a thunk t, lazy returns a new thunk that, when invoked, returns the value of invoking t. Once computed, the value is saved in a local variable so that the computation need not be performed again. A boolean flag is used to record whether t has been invoked and its value saved.
(define lazy
(lambda (t)
(let ([val #f] [flag #f])
(lambda ()
(if (not flag)
(begin (set! val (t))
(set! flag #t)))
val))))
这里出现的语法形式begin，从左到右求值它的子表达式，返回最后一个子表达式的值。就象 let和lambda的 body 一样。我们也看到了，if表达式的 else子句可以省略。只有当if表达式的值可以丢弃的时候才应该这样做，在lazy函数里就是这个情况。
需要长时间计算的情况下，惰性求值很有用，通过延迟计算，我们完全可以避免计算，通过保存值，我们可以避免重复计算。
lazy函数的操作可以通过传递给它一个打印消息的 thunk 来很好地说明。
[注：在函数式编程语言里 thunk 这个术语通常表示没有参数的函数，而且通常是以匿名函数的形式传递到别的函数里去]
(define p
(lazy (lambda ()
(display "Ouch!")
(newline)
"got me")))
当p第一次被调用，它打印出消息 "Ouch!", 然后返回字符串 "got me"。当它再次被调用，将不再打印消息，只是返回一个字符串 "got me"。display及newline过程是我们看到的输入/输出的第一个例子；display将字符串打印成不含双引号的样子，而newline则输出一个换行符。
为了进一步说明set!的使用，我们来考虑实现一个栈数据结构（后进先出）。一个栈对象接受如下4个消息：empty?，如果栈空，返回#t，否则返回#f；push!,压栈操作，将一个对象存入栈中；top，返回栈顶的对象；pop!，从栈里面删除栈顶的对象。下面的make-stack函数每次调用时创建一个新的栈。
(define make-stack
(lambda ()
(let ([ls '()])
(lambda (msg . args)
(cond
[(eqv? msg 'empty?) (null? ls)]
[(eqv? msg 'push!) (set! ls (cons (car args) ls))]
[(eqv? msg 'top) (car ls)]
[(eqv? msg 'pop!) (set! ls (cdr ls))]
[else "oops"])))))
栈存储在一个绑定为ls的列表里面，set!用于改变绑定的操作push!及pop!。注意内层的 lambda 使用了一个不是很合适的方法，将所有参数的列表绑定到一个变量args上面，但是只使用了其中的第一个（push!的时候，只是人 args里拿出car来cons到列表中，其余的都被丢弃了）。在这里它是有用的，因为函数的参数并不固定，empty?, top, pop!只有一个参数，就是消息本身，而push!需要两个参数，除了消息，还需要另外一个参数，就是将到压栈的对象。
(define stack1 (make-stack))
(define stack2 (make-stack))
(list (stack1 'empty?) (stack2 'empty?)) => (#t #t)
(stack1 'push! 'a)
(list (stack1 'empty?) (stack2 'empty?)) => (#f #t)
(stack1 'push! 'b)
(stack2 'push! 'c)
(stack1 'top) => b
(stack2 'top) => c
(stack1 'pop!)
(stack1 'top) => a
(list (stack1 'empty?) (stack2 'empty?)) =>s (#f #f)
(stack1 'pop!)
(list (stack1 'empty?) (stack2 'empty?)) => (#t #f)
与通过 make-counter产生的计数器一样，每个栈内部维护的状态只能从通过对象本身直接访问。这样做一个重要的好处是，我们可以改变栈的内部结构，而不会影响到其外部行为。比如将保存数据的列表改为向量（参见6.9节）。因为该对象的行为是已知的抽象（不是操作），它被称为一个抽象的对象。更多的关于抽象对象的内容参见12.8节.
除了改变变量的值，我们也可以分别改变一个 pair 的 car 及 cdr 字段。通过 set-car!以及set-cdr!
(define p (list 1 2 3))
(set-car! (cdr p) 'two)
p => (1 two 3)
(set-cdr! p '())
p => (1)
我们可以通过这些操作来实现一个队列数据结构，队列和栈很相似，除了新的元素添加到一端，而从另一端取出元素。即先进先出。下面的队列实现使用了一种叫做tconc的结构。tconc 由两部分构成：一个非空列表，以及一个 header。header 是一个 pair, car 指向列表中的第一个 pair, header 的 cdr 指向列表中的最后一个 pair。
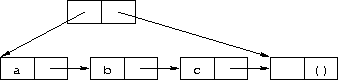
列表最后的元素是一个占位符，并非队列的一部分。
列表可以有 4 种操作，分别定义在下面：make-queue, 构建一个队列；putq!, 往队列的末尾添加一个元素；getq，从队列前方取出一个元素；delq!，移除队列前方的元素。
(define make-queue
(lambda ()
(let ([end (cons 'ignored) '()])
(cons end end))))
(define putq!
(lambda (q v)
(let ([end (cons 'ignored '())])
(set-car! (cdr q) v)
(set-cdr! (cdr q) end)
(set-cdr! q end))))
(define getq
(lambda (q)
(car (car q))))
(define delq!
(lambda (q)
(set-car! q (cdr (cdr q)))))
除了 putq! 外都是些简单的操作。putq!修改队列最后的 pair 来容纳新的值，然后将一个新的结尾 pair 添加到队列里。
(putq! myq 'a)
(putq! myq 'b)
(getq myq) => a
(delq! myq)
(getq myq) => b
(delq! myq)
(putq! myq 'c)
(putq! myq 'd)
(getq myq) => c
(delq! myq)
(getq myq) => d